Microsoft Word - O_ETRU.doc
|
|
|
- Grega Majcen
- pred 4 leti
- Pregledov:
Transkripcija
1 UNIVERZ V LJUBLJNI FKULTET Z MTEMTIKO IN FIZIKO ODDELEK Z FIZIKO O ETRU Seminar 4/6 vtor: Nina Jereb Mentor: dr. Janez Strnad Eter je eden izmed tistih pojmov, ki so v fiziki igrali pomembno vlogo, kljub temu da nima natančnega operacijskega pomena. Seminar ga obravnava z zgodovinskega gledišča. Vidimo, da je tesno povezan z razvojem spoznanj o svetlobi in z teorijo relativnosti. Ljubljana,
2 KZLO UVOD... 3 ZČETKI RZMIŠLJNJ O ETRU... 3 ETER V FIZIKI... 4 DELČN TEORIJ PREVLD... 5 ZČETKI VLOVNE TEORIJE... 5 FRESNELOV ENČB (hitrost svetlobe v gibajoči se snovi)... 6 Veljavna teorija zgrajena na napačni predstavi?... 6 li naj enačbi verjamemo?... 7 Od kod ujemanje?... 8 SVETLOB KOT TRNSVERZLNO VLOVNJE ETR... 8 FRESNELOVE ENČBE ODBOJ... 9 TEŽVE Z ETROM KONEC ETR?... 1 ZKLJUČEK LITERTUR... 14
3 UVOD Predstava o etru se je skozi zgodovino močno spreminjala. Od 17 stol. dalje ga srečujemo v povezavi z razmišljanji o širjenju svetlobe.[1],[],[3] Kasneje so fiziki misel o etru, kot mediju za potovanje svetlobe, opustili. Presenetljivo je, da nekatere napovedi, ki so zrasle na tej predpostavki, še danes veljajo. (Snellov lomni zakon, Fresnelove enačbe, hitrost potovanja svetlobe v gibajoči se snovi v 1. redu,... ).[1],[4] Razmišljanje o etru nas veliko nauči o poteku fizikalnih odkritij in uveljavljanju novih teorij. Nove ideje niso takoj sprejete in tudi napačne predpostavke prispevajo k razvoju znanosti.[5],[6] Odkrivanje, spreminjanje obstoječih pogledov in razvijanje novih teorij je zapleten proces, v katerega je vključeno človeštvo kot celota. Večkrat pripišemo zasluge za nova spoznanja eni sami osebi (ali majhni skupini). Zgodovino poenostavimo, da postane bolj pregledna in lažje razumljiva, zavedati pa se moramo, da jo na ta način tudi popačimo. Že res, da so v razvoju fizike nekatere osebnosti imele vidnejšo vlogo, a delovale so v okviru tedanjega časa in nekako poosebljajo tok misli in idej.[7],[8] V tem seminarju se želim vrniti v čas in pogledati, kako so si nekoč pomagali z etrom. ZČETKI RZMIŠLJNJ O ETRU Ko gledamo nazaj na zgodovino, ne moremo odmisliti današnjega znanja. Zgodovino doživljamo skozi oči današnje fizike in sodobnih predstav o svetu. To, kar se nam danes zdi samo po sebi umevno, včasih ni bilo tako. Temu kaže nameniti pozornost. Od kod izvirajo naše predstave? Pojem eter se je pojavil v času starih Grkov. ristotel je razlagal, da je materija zgrajena iz štirih elementov: zemlja, ogenj, voda in zrak. To naj bi veljalo za svet pod Luno, nespremenljiv nebesni svod nad Luno, pa naj bi bil zgrajen iz nečesa drugega, kar je poimenoval eter. ristotel je bil prepričan, da v naravi ni praznine. Na vprašanje kako vidimo, je odgovoril, Slika 1: ristotel da se od predmeta prenaša gibanje do očesa preko etra. V tem nekateri vidijo celo začetek valovne teorije svetlobe [1], vendar se moramo zavedati, da so bile predstave o svetlobi pri ristotelu še zelo meglene. O svetlobi, kot valovanju - sinusnem nihanju, je šele mnogo kasneje prvič govoril Young (19. stol.). Ideje, 3
4 da je svetloba valovanje ni potegnil kar iz niča. Razvoj spoznanj o svetlobi je tesno povezan ravno z zamislijo o etru, ki se je najprej pojavil v filozofiji, kasneje pa ga je posvojila še fizika. ETER V FIZIKI Slika : Vrtinci etra po Descartesovi predstavi. Na sredi vrtinca je osončje. [1] Pojem etra je v fiziko vpeljal René Descartes v tridesetih letih 17. stoletja. Tudi on je menil, da v naravi ni praznine. Trdil je, da telo deluje na drugo telo le preko dotika. Mislil si je, da telesa iz etra, ki naj bi bil nekakšna snov, izpolnjujejo ves prostor. Ta telesa, ki so se zaradi trenja obrusila, obstajajo v treh velikostih. Najmanjša so svetleča in sestavljajo zvezde. Srednje velika telesa so prozorna in napolnjujejo prostor med planeti in zvezdami. Največja telesa sestavljajo planete. Prozorna telesa se vrtinčijo in poganjajo planete okoli Sonca, podobno kot vrtinci vode poganjajo deščice.[] V tej razpravi so najzanimivejša srednje velika, prozorna, telesa. Preko njih naj bi se prenašala svetloba v obliki nekakšnega tlačnega vala. Idejo je razvil Christian Huygens, Descartesov mlajši somišljenik. V Razpravi o svetlobi (Traité de la lumiere, 1678) je sprejel zamisel, da je svetloba motnja, ki se longitudinalno širi po etru[1][] na podoben način kot zvok, le da veliko hitreje. Po poskusih Evangeliste Torricellija so takrat že vedeli, da gre, za razliko od zvoka, svetloba tudi skozi prazen prostor. Pri longitudinalnem valovanju ni imel v mislih periodičnih valov (ni se trudil pojasniti interferenco, ki jo je že pred letom 1663 opazil Francesco Maria Grimaldi). Svetloba je bila zanj le motnja. Povezoval jo je z mehaničnim modelom z vrsto krogel, po katerih se prenaša motnja. Svetlobo prenaša po vakuumu eter, ki je sestavljen iz majhnih delcev. Po prozornih snoveh jo prenaša ali samo snov, ali samo eter, ali pa oboje. Preko možnosti, da bi jo hkrati prenašala tako eter kot snov, je poskušal pojasniti dvojni lom (l ga je odkril Erasmus Bartholinus). Tako razlago je imel za najbolj verjetno, a pri njej ni vztrajal. [1] Z etrom je razložil Snellov lomni zakon. Trdil je, da iz vsake točke valovnega čela izhajajo krogelna elementarna valovanja. Ovojnica elementarnih valov je novo valovno čelo [7]. Temu danes pravimo Huygensovo načelo. Iz tega načela sledi, da je hitrost v snovi manjša, če se 4
5 žarek lomi proti pravokotnici. Menil je, da svetloba v snovi počasneje potuje, ker eterske delce v njej motijo delci snovi [1]. DELČN TEORIJ PREVLD Valovna teorija je imela nasprotnike zagovornike delčne teorije. Prvi med njimi je bil sir Isaac Newton. Menil je, da je svetloba sestavljena iz številnih majhnih delčkov, ki jih prozorna snov privlači. Zaradi močnega Newtonovega vpliva (imel je velik ugled), se Huygensove ideje ob svojem času niso uveljavile. V 18. stoletju je prevladala delčna teorija svetlobe. Le to so podprla tudi odkritja Jamesa Bradleya (slika 3). Leta 178 je poročal, da opišejo zvezde, ki jih vidimo pod pravim kotom glede na gibanje Zemlje okoli Sonca, navidezen krog, katerega radij vidimo pod kotom ločnih sekund. Temu kotu pravimo zvezdna aberacija. Brandley je ta pojav razložil s pomočjo Newtonove delčne teorije. Svetlobo je opisal kot»dež delcev«. Če pada dež navpično z hitrostjo v dež mi pa se premikamo s hitrostjo v, moramo držati dežnik pod kotom arctg(v/v dež ). Če prevedemo to na gibanje zemlje in svetlobo zvezd dobimo izraz α = arctg( v / c), kjer je α aberacijski kot, v je hitrost potovanja Zemlje okoli Sonca, c pa hitrost svetlobe. Iz hitrosti Zemlje in aberacijskim kotom je ocenil hitrost svetlobe. Za v vstavimo hitrost gibanja Zemlje okoli Sonca v=3 km/s, aberacija α=,6''. Slika 3: James Bradley in»zvezdna aberacija«. c = v / α 3km / s. ZČETKI VLOVNE TEORIJE Valovno teorijo sta na začetku 19. stoletja oživela Thomas Young in Fresnel. Za razliko od Huygensa, ki je smatral, da je svetloba le motnja, ki potuje po etru, so v tem času, več kot stoletje kasneje, govorili o valovanju v pravem smislu besede (sinusno valovanje). 5
6 Leta 18 je Young prvič v celoti objavil svoje načelo interference:» če dva dela iste svetlobe dospeta do očesa po različnih poteh, postane svetloba najmočnejša, če je razlika večkratnik določene dolžine, in najmanj močna v vmesnem stanju interferirajočih delov: in ta dolžina je različna za svetlobo različnih barv.«young je z valovanjem pojasnil tudi kolobarje na robovih senc. Vendar je mislil, da je valovanje longitudinalno. Dvojnega loma zato ni znal razložiti. Pristašev delčne teorije je bilo še zmeraj veliko. Valovni teoriji je še posebej slabo kazalo, ko je Poisson ugotovil, da le-ta napoveduje na interferenčni sliki za okroglo oviro svetlo pego. Šele ko je Fresnel to z eksperimentom pokazal, je teorija obveljala. FRESNELOV ENČB (hitrost svetlobe v gibajoči se snovi) Veljavna teorija zgrajena na napačni predstavi? Po mnenju Fresnela naj bi eter»šel skozi snov vseh teles z malo ali nič upora, nekako tako neovirano, kot gre veter skozi nasad dreves«[1]. S pomočjo te predstave je prišel do še danes veljavne enačbe, ki opisuje hitrost gibanja svetlobe v gibajočem se mediju. Upošteval je enačbo n = c / c. Hitrost potovanja svetlobe po etru si je zamislil po analogiji z zvokom: c = G / ρ. G je strižni modul etra, ρ pa njegova gostota v snovi. Iz tega je dobil kvadratno zvezo ρ = ρ n, kjer je ρ manjša gostota etra v vakuumu. Gostejša telesa imajo torej večji lomni količnik in po njih svetloba počasneje potuje. Strižni modul etra naj bi bil v snovi in v prostoru enak. Po Fresnelovi predstavi se telo nemoteno giblje po etru, ki miruje. Presežek etra ρ ρ ) se giblje s hitrostjo v. Hitrost»težišča«je potemtakem: ( V[( ρ ρ ) v + ρ ] ρ ρ 1 = v = (1 ) v = k F v. (1) V[( ρ ρ ) + ρ ] ρ n 6
7 Pri tem je = (1 1/ n ) Fresnelov koeficient. Snov naj se giblje v smeri svetlobe. Če k F želimo v njej izračunati hitrost svetlobe, seštejemo hitrost svetlobe v tem mediju in hitrost»težišča«, torej c / n + k v. Motivacija za nastanek te teorije je bila zvezdna aberacija, oz. F vprašanje, kaj se zgodi npr. s Snellovim lomnim zakonom v gibajočem se koordinatnem sistemu. li naj enačbi verjamemo? Fresnelova enačba za hitrost svetlobe se v linearnem približku ujema z enačbo posebne teorije relativnosti (). v ( v + v ) x o x = () 1+ v xvo c v x je hitrost v opazovalnem sistemu S. v' x je hitrost v sistemu S', ki se glede na S giblje s hitrostjo v v smeri osi x = x'. Če v to enačbo vstavimo c ' = in v = v, dobimo: n v x co + v c 1 v = n x = v (3) v n 1+ n c n Enačba (3) pokaže, da se rezultat eterske teorije v linearnem približku ujema z rezultatom posebne teorije relativnosti. Fresnelovo enačbo je s svojimi merjenji podprl Hippolyte Fizeau. Leta 1851 je naredil eksperiment, kjer je po stekleni cevi v obliki črke U potiskal vodo (slika 4). Svetlobo je ločil na dva delna curka. Vsak curek je poslal skozi svoj krak cevi. Prvi je torej potoval v smeri gibanja vode, drugi pa v nasprotni smeri. Delna curka je na drugi strani speljal v daljnogled, kjer je opazoval interferenčno sliko svetlih in temnih prog. [] 7
8 Slika 4: Fizeaujev interferometer z režama (iz leta 1851) Dolžina cevi je bila 1,5m, hitrost vode je bila 7m/s. [4] V vodi, ki teče s hitrostjo v, v smeri curka svetlobe, je hitrost svetlobe c / n + k F v. V vodi, ki teče v nasprotni smeri, je hitrost svetlobe c / n k v. Zaradi tega je valovanje v drugem kraku zakasnjeno, kar lahko na zaslonu zaznamo. Fizeau je primerjal lego prog, ko je voda mirovala in ko je tekla z različnimi hitrostmi. Izmerjeni Fresnelov koeficient je bil,46. Za vodo z lomnim kvocientom 4/3 je izračunan Fresnelov kvocient,438. Tej vrednosti sta se kasneje še bolj približala Michelson in Morley z izboljšano verzijo Fizeaujevega poiskusa. Njuna izmerjena vrednost je bila,434, kar od izračunane vrednost odstopa le za en odstotek. F Od kod ujemanje? Predpostavka Frenelesove teorije je, da se svetloba giblje s hitrostjo c = G / ρ. Danes bi rekli, da se svetloba v mediju giblje s hitrostjo 1 c =. Vemo, da je ε povezan z ρ. εε µµ Fresnel je privzel, da se strižni modul etra G pri prehodu v snov ne spremeni. To se ravno ujame z dejstvom, da je večina prozornih snovi paramagnetnih in je torej µ 1. Torej se tudi magnetna subsepscibilnost pri prehodu v prozorno snov ne spremeni. Naj to jemljemo kot srečno naključje ali Fresnelovo intuicijo, ostaja dejstvo, da je njegova enačba še danes uporabna. SVETLOB KOT TRNSVERZLNO VLOVNJE ETR Polarizacija in dvojni lom še zmeraj nista bila pojasnjena. Fresnel je že pred Youngom razmišljal o transverzalnem valovanju in ga je leta 1817 usvojil brez pomislekov. Young tega ni bil zmožen. Menil je, da bi moral eter imeti preveč nenavadne lastnosti. Še leta 183 je zapisal:»treba bi bilo sklepati, da svetlonosni eter, ki izpolnjuje ves prostor in prežema 8
9 skoraj vse snovi, ni samo močno prozoren, ampak absolutno trden!!!«opustil je delo s svetlobo in se vrnil k nekaterim prejšnjim raziskovanjem. Eter ob predpostavki, da se po njem širi transverzalno valovanje, dobi nenavadne lastnosti. Imeti mora lastnosti trdnine, da se preko njega transverzalno valovanje sploh lahko prenaša. Da svetloba lahko potuje s tako veliko hitrostjo, mora imeti ogromen strižni modul. Ob predpostavki, da ima gostoto zraka, mora biti strižni modul več milijon-krat večji od strižnega modula jekla. Hkrati bi moral biti brezmasen, in popolnoma neviskozen, saj bi v nasprotnem primeru opazno vplival na orbite planetov. Izgledalo je še, da je popolnoma prosojen, da ni nobenega sipanja, je nestisljiv in zvezen na izredno majhni skali. [3] Fresnel si z nenavadnimi lastnostmi ni preveč belil glave. Bil je teoretik. Ni se trudil sestaviti mehaničnega modela in se tudi ni ubadal s tem, kako je mogoče, da ima eter tako čudne lastnosti. Napisal je teorijo, pa si je mislil, da bo že čas pokazal, kaj za tem tiči. To se je tudi res zgodilo. Mnoge njegove teorije so še danes veljavne, pa čeprav so kasneje ovrgli idejo o etru kot mediju za prenašanje svetlobe. Z upoštevanjem robnih pogojev za vzdolžno in prečno komponento premika v etru je izpeljal Fresnelove enačbe. FRESNELOVE ENČBE ODBOJ Fresnel je svoje enačbe izpeljal na drugačen način, kot to delamo danes. Maxwellovega elektromagnetizma seveda ni poznal. Pri izpeljavi je imel v mislih mehanično valovanje etra. Uporabil je zakon o ohranitvi energije in predpostavko, da je vsota vzdolžnih hitrosti»etrskih delcev«na eni strani meje enaka hitrostim na drugi strani meje. Enačba (4) govori o ohranitvi energije. Imejmo snop svetlobe. Prvi del se lomi, drugi del se odbije. Po Fresnelovi predstavi v vpadnem snopu nihajo delci etra z amplitudo. V lomljenem snopu nihajo z amplitudo 1, v odbitem pa z amplitudo. Energija je sorazmerna s kvadratom amplitude. Valovna fronta se pri prehodu čez mejo zlomi. Energija vpadnega snopa mora biti enaka vsoti energij odbitega in lomljenega snopa. Torej mora veljati enakost (4). Z uporabo lomnega zakona pridemo do enačbe (5). 9
10 = 1 ρ n1 ρ n (4) ρ n + 1 = 1 cos β sinα + cosα sin β (5) Drugi pogoj je, da je vsota vzdolžnih hitrosti na eni strani meje enaka hitrostim na drugi strani meje. Hitrost pa je sorazmerna z amplitudo (6). v = πν s v s (6) Če je v pravokotna na vpadno ravnino: V primeru, ko je v pravokotna na vpadno ravnino (slika 5), se hitrosti oz. amplitude enostavno seštejejo (7). v + v = + = (7) v1 1 1 sin β cosα = (8) sin( α + β ) Slika 5 sin( β α) = sin( α + β ) (9) Iz enačb (5) in (7) dobimo enačbi (8) in (9), Fresnelovi enačbi za propustnost in odbojnost. Danes uporabljamo te enačbe pri TE valovanju, torej, ko je E pravokoten na vpadno ravnino. Če je v v vpadni ravnini: Podobno računamo, če je v v vpadni ravnini, le da hitrost razstavimo na komponente in vzamemo le tisto komponento, ki je usmerjena vzdolž meje (slika 6). ( 1 1 v v ) cosα = v cos β ( ) cosα = cos β (1) 1
11 1 sin β cosα = sinα cosα + sin β cos β sinα cosα sin β cos β = sinα cosα + sin β cos β (11) (1) Slika 6 Iz enačb (5) in (1) dobimo enačbi (11) in (1), Danes uporabljamo te enačbe pri TM valovanju, torej, ko je B pravokoten na vpadno ravnino. Fresnelove enačbe so ostale enake, a smo jih reinterpretitali. TEŽVE Z ETROM Fiziki so se zavedali težav in nerazrešenih vprašanj v zvezi z etrom, a je bila ta predstava v fiziko že tako močno vpletena, da se je niso mogli kar tako znebiti. V zgodnjih letih dvajsetega stoletja je bila teorija o etru v težavah. Vedno več je bilo eksperimentov, ki so poskušali zaznati gibanje zemlje glede na eter. Neuspešno! Pojavile so se razne razlage, zakaj tega gibanja niso zaznali. Ena od idej je bila, da Zemlja vleče eter s sabo (torej se ne gibljeta drug glede na drugega), a je razlaga zelo zapletena in zahteva mnogo fizikalnih predpostavk. Elegantnejšo rešitev sta našla Lorentz in Fitzgerald (krčenje razdalj). Specialna teorija relativnosti operira z enako matematiko brez uvedbe etra.[3] Ključna težava teorije o etru je neujemanje Newtonove mehanike in Maxwellovega elektromagnetizma. Enačbe Newtonove mehanike so invariantne na Galilejevo transformacijo, med tem ko enačbe elektromagnetizma niso. Z drugimi besedami to pomeni, da bi veljali mehanični zakoni v vseh nepospešenih opazovalnih sistemih (trajektorija poševnega meta je npr. enaka na zemlji in na letalu), zakoni za svetlobo pa bi se spremenili. 11
12 Le ti naj bi veljali le v opazovalnem sistemu, kjer eter miruje. Maxwellov elektromagnetizem je namreč zahteval eno samo, univerzalno, hitrost svetlobe.[3] Izid Michelsonovega in Morleyevega poskusa je močno zamajal teorijo o mirujočem etru. Poskušali so jo sicer še oživeti z razlagami, da se eter lepi na zemeljsko površje, a so te ideje počasi zamrle. Leta 1889 je G. F. Fitzgerald domneval, da se vse dolžine na zemlji skrčijo za faktor 1/ ( 1 v / c ), kjer je v hitrost zemlje v etru [4]. Enačbe je naprej razvijal H.. Lorentz in drugi. V Lorentzovih transformacijah niso videli fizikalnega pomena ampak le matematično orodje. Pojma etra so se še naprej oklepali. Iz fizike ga je, vsaj za nekaj časa, izrinil šele Einstein s svojo teorijo relativnosti.» Pokazalo se bo, da je odveč uvajati `svetlobni eter` toliko, kolikor v predstavi, ki jo bomo razvili, ne bomo uvedli `absolutno mirujočega prostora` s posebnimi lastnostmi «. Einstein, Zur Elektrodynamik bewegter Körper, nnalen der Physik 17(195)891 KONEC ETR? V fiziki se še vedno govori o etru, le da mu pripisujejo drugačen pomen. Pojavlja se v kvantni teoriji polja in povsod drugod v zvezi z dinamičnimi lastnostmi prostora. (npr. nastajanje parov delec-antidelec, )»Vakuum ali eter ima dinamične lastnosti, ki jih pred časom niso niti slutili, in vse kaže, da bo imel v prihodnosti še pomembno vlogo.«ja. B. Zeldovič» V splošni teoriji relativnosti lahko rečemo, da ima prostor fizikalne lastnosti. V tem smislu tedaj obstaja eter. V tej teoriji si ni mogoče zamisliti prostora brez etra, ker po takem prostoru nebi potovala svetloba in v njem nebi mogli obstajati merilniki za kraj in čas 1
13 (merilne palice in ure) ne krajevno časovni odmiki v fizikalnem smislu Toda temu etru ne smemo pripisati lastnosti teles z maso in misliti, da ga sestavljajo deli, ki bi jih lahko zasledovali v času. Ne moremo si misliti, da bi se lahko eter gibal «. Einstein» Posebej je pokazano, da je razvoj v tesnem stiku z Descartesovo zamislijo, da ne obstaja prazen prostor` «. Einstein ZKLJUČEK Videli smo, da je eter igral pomembno vlogo pri nastanku teorije o svetlobi. Le-ta se je skozi stoletja razvijala, se spreminjala. Nekatere ideje so se obdržale, druge je izbrisal čas, vseeno pa je vsaka doprinesla k razvoju fizike. Danes je zamisel o etru, kot absolutno mirujoči snovi, ovržena, a Fresnelove enačbe so se obdržale do danes v natančno taki obliki, kot jih je zapisal Fresnel. Eter se v novi preobleki vrača v fiziko [5]. li bo razmišljanje v tej smeri obrodilo sadove, bo pokazal čas. 13
14 LITERTUR [1] J. Strnad, Eter, Obzornik mat. fiz. 3(1983)97. [] J. Strnad, Eter in hitrost svetlobe, Fizika v šoli, letnik IX, št.1, oktober 5. [3] [4] J. Strnad, Michelsonovi poskusi, Obzornik mat. fiz. 3(1983) 6. [5] Detection of the nisotropy in the Cosmic Black body Radiation, Phys. Rev. Letters 39(1977)898. [6] J. Strnad, Razvoj fizike, Ljubljana: DZS, [7] Colin Ronan, Histoire mondiale des Sciences, Point Sciences [8] tlas klasične in moderne fizike, Ljubljana: DZS, [9] E. B. Sparberg, Misinterpretation of Theories of Light, m. J. Phys. 34(1966)377. [1] www71.univ-lyon1.fr/~fdenis/club_ee/cours/histoire1.html 14
SVETLOBA.dvi
 Stalno strokovno spopolnjevanje Oddelek za fiziko, Fakulteta za matematiko in fiziko Svetloba od antike do stimuliranega sevanja Janez Strnad Uvod V vsakdanjem življenju z vidom dobimo večino podrobnih
Stalno strokovno spopolnjevanje Oddelek za fiziko, Fakulteta za matematiko in fiziko Svetloba od antike do stimuliranega sevanja Janez Strnad Uvod V vsakdanjem življenju z vidom dobimo večino podrobnih
Univerza v Novi Gorici Fakulteta za aplikativno naravoslovje Fizika (I. stopnja) Mehanika 2014/2015 VAJE Gravitacija - ohranitveni zakoni
 Univerza v Novi Gorici Fakulteta za aplikativno naravoslovje Fizika (I. stopnja) Mehanika 2014/2015 VAJE 12. 11. 2014 Gravitacija - ohranitveni zakoni 1. Telo z maso M je sestavljeno iz dveh delov z masama
Univerza v Novi Gorici Fakulteta za aplikativno naravoslovje Fizika (I. stopnja) Mehanika 2014/2015 VAJE 12. 11. 2014 Gravitacija - ohranitveni zakoni 1. Telo z maso M je sestavljeno iz dveh delov z masama
1 Naloge iz Matematične fizike II /14 1. Enakomerno segreto kocko vržemo v hladnejšo vodo stalne temperature. Kako se spreminja s časom temperat
 1 Naloge iz Matematične fizike II - 2013/14 1. Enakomerno segreto kocko vržemo v hladnejšo vodo stalne temperature. Kako se spreminja s časom temperatura v kocki? Kakšna je časovna odvisnost toplotnega
1 Naloge iz Matematične fizike II - 2013/14 1. Enakomerno segreto kocko vržemo v hladnejšo vodo stalne temperature. Kako se spreminja s časom temperatura v kocki? Kakšna je časovna odvisnost toplotnega
Albert Einstein in teorija relativnosti
 Albert Einstein in teorija relativnosti Rojen 14. marca 1879 v judovski družini v Ulmu, odraščal pa je v Münchnu Obiskoval je katoliško osnovno šolo, na materino željo se je učil igrati violino Pri 15
Albert Einstein in teorija relativnosti Rojen 14. marca 1879 v judovski družini v Ulmu, odraščal pa je v Münchnu Obiskoval je katoliško osnovno šolo, na materino željo se je učil igrati violino Pri 15
7. tekmovanje v znanju astronomije 8. razred OŠ Državno tekmovanje, 9. januar 2016 REŠITVE NALOG IN TOČKOVNIK SKLOP A V sklopu A je pravilen odgovor o
 7. tekmovanje v znanju astronomije 8. razred OŠ Državno tekmovanje, 9. januar 2016 REŠITVE NALOG IN TOČKOVNIK SKLOP A V sklopu A je pravilen odgovor ovrednoten z 2 točkama; če ni obkrožen noben odgovor
7. tekmovanje v znanju astronomije 8. razred OŠ Državno tekmovanje, 9. januar 2016 REŠITVE NALOG IN TOČKOVNIK SKLOP A V sklopu A je pravilen odgovor ovrednoten z 2 točkama; če ni obkrožen noben odgovor
Fizikalne osnove svetlobe
 Fizikalne osnove svetlobe Svetloba Svetloba - skrivnostna in fascinantna spremljevalka človekove zgodovine Kako deluje vid? Svetloba in vid Dva pojma, ki sta danes neločljivo povezana. Vendar ni bilo vedno
Fizikalne osnove svetlobe Svetloba Svetloba - skrivnostna in fascinantna spremljevalka človekove zgodovine Kako deluje vid? Svetloba in vid Dva pojma, ki sta danes neločljivo povezana. Vendar ni bilo vedno
Matematika Diferencialne enačbe prvega reda (1) Reši diferencialne enačbe z ločljivimi spremenljivkami: (a) y = 2xy, (b) y tg x = y, (c) y = 2x(1 + y
 Matematika Diferencialne enačbe prvega reda (1) Reši diferencialne enačbe z ločljivimi spremenljivkami: (a) y = 2xy, (b) y tg x = y, (c) y = 2x(1 + y 2 ). Rešitev: Diferencialna enačba ima ločljive spremenljivke,
Matematika Diferencialne enačbe prvega reda (1) Reši diferencialne enačbe z ločljivimi spremenljivkami: (a) y = 2xy, (b) y tg x = y, (c) y = 2x(1 + y 2 ). Rešitev: Diferencialna enačba ima ločljive spremenljivke,
Mladi za napredek Maribora srečanje DOLŽINA»SPIRALE«Matematika Raziskovalna naloga Februar 2015
 Mladi za napredek Maribora 015 3. srečanje DOLŽINA»SPIRALE«Matematika Raziskovalna naloga Februar 015 Kazalo 1. Povzetek...3. Uvod...4 3. Spirala 1...5 4. Spirala...6 5. Spirala 3...8 6. Pitagorejsko drevo...10
Mladi za napredek Maribora 015 3. srečanje DOLŽINA»SPIRALE«Matematika Raziskovalna naloga Februar 015 Kazalo 1. Povzetek...3. Uvod...4 3. Spirala 1...5 4. Spirala...6 5. Spirala 3...8 6. Pitagorejsko drevo...10
ELEKTRIČNI NIHAJNI KROG TEORIJA Električni nihajni krog je električno vezje, ki služi za generacijo visokofrekvenče izmenične napetosti. V osnovi je "
 ELEKTRIČNI NIHAJNI KROG TEORIJA Električni nihajni krog je električno vezje, ki služi za generacijo visokofrekvenče izmenične napetosti. V osnovi je "električno" nihalo, sestavljeno iz vzporedne vezave
ELEKTRIČNI NIHAJNI KROG TEORIJA Električni nihajni krog je električno vezje, ki služi za generacijo visokofrekvenče izmenične napetosti. V osnovi je "električno" nihalo, sestavljeno iz vzporedne vezave
resitve.dvi
 FAKULTETA ZA STROJNISTVO Matematika Pisni izpit. junij 22 Ime in priimek Vpisna st Navodila Pazljivo preberite besedilo naloge, preden se lotite resevanja. Veljale bodo samo resitve na papirju, kjer so
FAKULTETA ZA STROJNISTVO Matematika Pisni izpit. junij 22 Ime in priimek Vpisna st Navodila Pazljivo preberite besedilo naloge, preden se lotite resevanja. Veljale bodo samo resitve na papirju, kjer so
RAČUNALNIŠKA ORODJA V MATEMATIKI
 DEFINICIJA V PARAVOKOTNEM TRIKOTNIKU DEFINICIJA NA ENOTSKI KROŢNICI GRAFI IN LASTNOSTI SINUSA IN KOSINUSA POMEMBNEJŠE FORMULE Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z
DEFINICIJA V PARAVOKOTNEM TRIKOTNIKU DEFINICIJA NA ENOTSKI KROŢNICI GRAFI IN LASTNOSTI SINUSA IN KOSINUSA POMEMBNEJŠE FORMULE Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z
ANALITIČNA GEOMETRIJA V RAVNINI
 3. Analitična geometrija v ravnini Osnovna ideja analitične geometrije je v tem, da vaskemu geometrijskemu objektu (točki, premici,...) pridružimo števila oz koordinate, ki ta objekt popolnoma popisujejo.
3. Analitična geometrija v ravnini Osnovna ideja analitične geometrije je v tem, da vaskemu geometrijskemu objektu (točki, premici,...) pridružimo števila oz koordinate, ki ta objekt popolnoma popisujejo.
FIZIKA IN ARHITEKTURA SKOZI NAŠA UŠESA
 FIZIKA IN ARHITEKTURA SKOZI NAŠA UŠESA SE SPOMNITE SREDNJEŠOLSKE FIZIKE IN BIOLOGIJE? Saša Galonja univ. dipl. inž. arh. ZAPS marec, april 2012 Vsebina Kaj je zvok? Kako slišimo? Arhitekturna akustika
FIZIKA IN ARHITEKTURA SKOZI NAŠA UŠESA SE SPOMNITE SREDNJEŠOLSKE FIZIKE IN BIOLOGIJE? Saša Galonja univ. dipl. inž. arh. ZAPS marec, april 2012 Vsebina Kaj je zvok? Kako slišimo? Arhitekturna akustika
1 Merjenje sil in snovnih lastnosti 1.1 Merjenje sil z računalnikom Umeritev senzorja Senzor za merjenje sile pretvarja silo v električno napetost. Si
 1 Merjenje sil in snovnih lastnosti 11 Merjenje sil z računalnikom Umeritev senzorja Senzor za merjenje sile pretvarja silo v električno napetost Signal vodimo do računalnika, ki prikaže časovno odvisnost
1 Merjenje sil in snovnih lastnosti 11 Merjenje sil z računalnikom Umeritev senzorja Senzor za merjenje sile pretvarja silo v električno napetost Signal vodimo do računalnika, ki prikaže časovno odvisnost
Klasična teorija polja L. D. Landau in E. M. Lifšic Inštitut za fizikalne naloge, Akademija za znanost ZSSR, Moskva Prevod: Rok Žitko, IJS 29. decembe
 Klasična teorija polja L. D. Landau in E. M. Lifšic Inštitut za fizikalne naloge, Akademija za znanost ZSSR, Moskva Prevod: Rok Žitko, IJS 29. december 2003 Kazalo 1 Načelo relativnosti 6 1 Hitrost širjenja
Klasična teorija polja L. D. Landau in E. M. Lifšic Inštitut za fizikalne naloge, Akademija za znanost ZSSR, Moskva Prevod: Rok Žitko, IJS 29. december 2003 Kazalo 1 Načelo relativnosti 6 1 Hitrost širjenja
7. VAJA A. ENAČBA ZBIRALNE LEČE
 7. VAJA A. ENAČBA ZBIRALNE LEČE 1. UVOD Enačbo leče dobimo navadno s pomočjo geometrijskih konstrukcij. V našem primeru bomo do te enačbe prišli eksperimentalno, z merjenjem razdalj a in b. 2. NALOGA Izračunaj
7. VAJA A. ENAČBA ZBIRALNE LEČE 1. UVOD Enačbo leče dobimo navadno s pomočjo geometrijskih konstrukcij. V našem primeru bomo do te enačbe prišli eksperimentalno, z merjenjem razdalj a in b. 2. NALOGA Izračunaj
Vrste
 Matematika 1 17. - 24. november 2009 Funkcija, ki ni algebraična, se imenuje transcendentna funkcija. Podrobneje si bomo ogledali naslednje transcendentne funkcije: eksponentno, logaritemsko, kotne, ciklometrične,
Matematika 1 17. - 24. november 2009 Funkcija, ki ni algebraična, se imenuje transcendentna funkcija. Podrobneje si bomo ogledali naslednje transcendentne funkcije: eksponentno, logaritemsko, kotne, ciklometrične,
Khamikaze - Astro - Vogel 2011.indd
 VESOLJE, KI ME PREVZEMA SREČANJE PRIJATELJEV RADIA OGNJIŠČE VOGEL 2011 utrinki Kje smo? Živimo v prostoru in času. Smo del narave (Stvarstva) in zato razmišljajmo o njej. Doma smo v galaksiji Rimska cesta
VESOLJE, KI ME PREVZEMA SREČANJE PRIJATELJEV RADIA OGNJIŠČE VOGEL 2011 utrinki Kje smo? Živimo v prostoru in času. Smo del narave (Stvarstva) in zato razmišljajmo o njej. Doma smo v galaksiji Rimska cesta
KAKO VELIKA SO ŠTEVILA
 KAKO VELIKA SO ŠTEVILA V teh vajah i bomo ogledali nekaj primerov, ko v vakdanjem življenju naletimo na zelo velika števila. Uporabili bomo zmožnot programa DERIVE, da zna računati poljubno velikimi celimi
KAKO VELIKA SO ŠTEVILA V teh vajah i bomo ogledali nekaj primerov, ko v vakdanjem življenju naletimo na zelo velika števila. Uporabili bomo zmožnot programa DERIVE, da zna računati poljubno velikimi celimi
PowerPointova predstavitev
 Obravnava kotov za učence s posebnimi potrebami Reading of angles for pupils with special needs Petra Premrl OŠ Danila Lokarja Ajdovščina OSNOVNA ŠOLA ENAKOVREDNI IZOBRAZBENI STANDARD NIŽJI IZOBRAZBENI
Obravnava kotov za učence s posebnimi potrebami Reading of angles for pupils with special needs Petra Premrl OŠ Danila Lokarja Ajdovščina OSNOVNA ŠOLA ENAKOVREDNI IZOBRAZBENI STANDARD NIŽJI IZOBRAZBENI
Poslovilno predavanje
 Poslovilno predavanje Matematične teme z didaktiko Marko Razpet, Pedagoška fakulteta Ljubljana, 20. november 2014 1 / 32 Naše skupne ure Matematične tehnologije 2011/12 Funkcije več spremenljivk 2011/12
Poslovilno predavanje Matematične teme z didaktiko Marko Razpet, Pedagoška fakulteta Ljubljana, 20. november 2014 1 / 32 Naše skupne ure Matematične tehnologije 2011/12 Funkcije več spremenljivk 2011/12
dr. Andreja Šarlah Teorijska fizika II (FMF, Pedagoška fizika, 2010/11) kolokviji in izpiti Vsebina Kvantna mehanika 2 1. kolokvij 2 2. kolokvij 4 1.
 dr. Andreja Šarlah Teorijska fizika II (FMF, Pedagoška fizika, 2010/11) kolokviji in izpiti Vsebina Kvantna mehanika 2 1. kolokvij 2 2. kolokvij 4 1. izpit 5 2. izpit 6 3. izpit (2014) 7 Termodinamika
dr. Andreja Šarlah Teorijska fizika II (FMF, Pedagoška fizika, 2010/11) kolokviji in izpiti Vsebina Kvantna mehanika 2 1. kolokvij 2 2. kolokvij 4 1. izpit 5 2. izpit 6 3. izpit (2014) 7 Termodinamika
Poskusi s kondenzatorji
 Poskusi s kondenzatorji Samo Lasič, Fakulteta za Matematiko in Fiziko, Oddelek za fiziko, Ljubljana Povzetek Opisani so nekateri poskusi s kondenzatorji, ki smo jih izvedli z merilnim vmesnikom LabPro.
Poskusi s kondenzatorji Samo Lasič, Fakulteta za Matematiko in Fiziko, Oddelek za fiziko, Ljubljana Povzetek Opisani so nekateri poskusi s kondenzatorji, ki smo jih izvedli z merilnim vmesnikom LabPro.
Osnove matematicne analize 2018/19
 Osnove matematične analize 2018/19 Neža Mramor Kosta Fakulteta za računalništvo in informatiko Univerza v Ljubljani Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja D f R priredi natanko
Osnove matematične analize 2018/19 Neža Mramor Kosta Fakulteta za računalništvo in informatiko Univerza v Ljubljani Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja D f R priredi natanko
Poročilo projekta : Učinkovita raba energije Primerjava klasične sončne elektrarne z sončno elektrarno ki sledi soncu. Cilj projekta: Cilj našega proj
 Poročilo projekta : Učinkovita raba energije Primerjava klasične sončne elektrarne z sončno elektrarno ki sledi soncu. Cilj projekta: Cilj našega projekta je bil izdelati učilo napravo za prikaz delovanja
Poročilo projekta : Učinkovita raba energije Primerjava klasične sončne elektrarne z sončno elektrarno ki sledi soncu. Cilj projekta: Cilj našega projekta je bil izdelati učilo napravo za prikaz delovanja
Ime in priimek: Vpisna št: FAKULTETA ZA MATEMATIKO IN FIZIKO Oddelek za matematiko Verjetnost Pisni izpit 5. februar 2018 Navodila Pazljivo preberite
 Ime in priimek: Vpisna št: FAKULTETA ZA MATEMATIKO IN FIZIKO Oddelek za matematiko Verjetnost Pisni izpit 5 februar 018 Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja Nalog je
Ime in priimek: Vpisna št: FAKULTETA ZA MATEMATIKO IN FIZIKO Oddelek za matematiko Verjetnost Pisni izpit 5 februar 018 Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja Nalog je
FGG13
 10.8 Metoda zveznega nadaljevanja To je metoda za reševanje nelinearne enačbe f(x) = 0. Če je težko poiskati začetni približek (še posebno pri nelinearnih sistemih), si lahko pomagamo z uvedbo dodatnega
10.8 Metoda zveznega nadaljevanja To je metoda za reševanje nelinearne enačbe f(x) = 0. Če je težko poiskati začetni približek (še posebno pri nelinearnih sistemih), si lahko pomagamo z uvedbo dodatnega
resitve.dvi
 FAKULTETA ZA STROJNIŠTVO Matematika 4 Pisni izpit 3. februar Ime in priimek: Vpisna št: Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja. Veljale bodo samo rešitve na papirju, kjer
FAKULTETA ZA STROJNIŠTVO Matematika 4 Pisni izpit 3. februar Ime in priimek: Vpisna št: Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja. Veljale bodo samo rešitve na papirju, kjer
BYOB Žogica v vesolju Besedilo naloge Glavna ideja igre je paziti, da žoga ne pade na tla igralne površine, pri tem pa zbrati čim več točk. Podobno ig
 BYOB Žogica v vesolju Besedilo naloge Glavna ideja igre je paziti, da žoga ne pade na tla igralne površe, pri tem pa zbrati čim več točk. Podobno igro najdemo tudi v knjigi Scratch (Lajovic, 2011), vendar
BYOB Žogica v vesolju Besedilo naloge Glavna ideja igre je paziti, da žoga ne pade na tla igralne površe, pri tem pa zbrati čim več točk. Podobno igro najdemo tudi v knjigi Scratch (Lajovic, 2011), vendar
predstavitev fakultete za matematiko 2017 A
 ZAKAJ ŠTUDIJ MATEMATIKE? Ker vam je všeč in vam gre dobro od rok! lepa, eksaktna veda, ki ne zastara matematičnoanalitično sklepanje je uporabno povsod matematiki so zaposljivi ZAKAJ V LJUBLJANI? najdaljša
ZAKAJ ŠTUDIJ MATEMATIKE? Ker vam je všeč in vam gre dobro od rok! lepa, eksaktna veda, ki ne zastara matematičnoanalitično sklepanje je uporabno povsod matematiki so zaposljivi ZAKAJ V LJUBLJANI? najdaljša
Univerza v Mariboru Fakulteta za naravoslovje in matematiko Oddelek za matematiko in računalništvo Enopredmetna matematika IZPIT IZ VERJETNOSTI IN STA
 Enopredmetna matematika IN STATISTIKE Maribor, 31. 01. 2012 1. Na voljo imamo kovanca tipa K 1 in K 2, katerih verjetnost, da pade grb, je p 1 in p 2. (a) Istočasno vržemo oba kovanca. Verjetnost, da je
Enopredmetna matematika IN STATISTIKE Maribor, 31. 01. 2012 1. Na voljo imamo kovanca tipa K 1 in K 2, katerih verjetnost, da pade grb, je p 1 in p 2. (a) Istočasno vržemo oba kovanca. Verjetnost, da je
DN080038_plonk plus fizika SS.indd
 razlage I formule I rešeni primeri I namigi I opozorila I tabele Srednješolski Plonk+ Fizika razlage formule rešeni primeri namigi opozorila tabele Avtor: Vasja Kožuh Strokovni pregled: dr. Gorazd Planinšič
razlage I formule I rešeni primeri I namigi I opozorila I tabele Srednješolski Plonk+ Fizika razlage formule rešeni primeri namigi opozorila tabele Avtor: Vasja Kožuh Strokovni pregled: dr. Gorazd Planinšič
PowerPoint Presentation
 Lasersko obarvanje kovin Motivacija: Z laserskim obsevanjem je možno spremeniti tudi barvo kovinskih površin, kar odpira povsem nove možnosti označevanja in dekoracije najrazličnejših sestavnih delov in
Lasersko obarvanje kovin Motivacija: Z laserskim obsevanjem je možno spremeniti tudi barvo kovinskih površin, kar odpira povsem nove možnosti označevanja in dekoracije najrazličnejših sestavnih delov in
Fizika2_stari_testi.DVI
 Stari pisni izpiti in kolokviji iz Fizike 2 na Fakulteti za elektrotehniko 6. november 2003 Tako, kot pri zbirki za Fiziko 1, so izpiti in kolokviji zbrani po študijskih letih (2002/2003, 2001/2002, 2000/2001).
Stari pisni izpiti in kolokviji iz Fizike 2 na Fakulteti za elektrotehniko 6. november 2003 Tako, kot pri zbirki za Fiziko 1, so izpiti in kolokviji zbrani po študijskih letih (2002/2003, 2001/2002, 2000/2001).
LABORATORIJSKE VAJE IZ FIZIKE
 UVOD LABORATORIJSKE VAJE IZ FIZIKE V tem šolskem letu ste se odločili za fiziko kot izbirni predmet. Laboratorijske vaje boste opravljali med poukom od začetka oktobra do konca aprila. Zunanji kandidati
UVOD LABORATORIJSKE VAJE IZ FIZIKE V tem šolskem letu ste se odločili za fiziko kot izbirni predmet. Laboratorijske vaje boste opravljali med poukom od začetka oktobra do konca aprila. Zunanji kandidati
FAKULTETA ZA STROJNIŠTVO Matematika 2 Pisni izpit 9. junij 2005 Ime in priimek: Vpisna št: Zaporedna številka izpita: Navodila Pazljivo preberite bese
 FAKULTETA ZA STROJNIŠTVO Matematika Pisni izpit 9. junij 005 Ime in priimek: Vpisna št: Zaporedna številka izpita: Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja. Veljale bodo
FAKULTETA ZA STROJNIŠTVO Matematika Pisni izpit 9. junij 005 Ime in priimek: Vpisna št: Zaporedna številka izpita: Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja. Veljale bodo
DELOVNI LIST ZA UČENCA
 ZRCALA - UVOD 1. polprepustno zrcalo 2. ploščice različnih barv ( risalni žebljički), svinčnik 3. ravnilo Na bel papir postavi polprepustno zrcalo in označi njegovo lego. Pred zrcalo postavi risalni žebljiček.
ZRCALA - UVOD 1. polprepustno zrcalo 2. ploščice različnih barv ( risalni žebljički), svinčnik 3. ravnilo Na bel papir postavi polprepustno zrcalo in označi njegovo lego. Pred zrcalo postavi risalni žebljiček.
Jupiter Seminarska naloga Šola: O.Š.Antona Martina Slomška Vrhnika Predmet: Fizika Copyright by: Doman Blagojević
 Jupiter Seminarska naloga Šola: O.Š.Antona Martina Slomška Vrhnika Predmet: Fizika Copyright by: Doman Blagojević www.cd-copy.tk Jupiter je peti planet od Sonca in daleč največji. Jupitrova masa je več
Jupiter Seminarska naloga Šola: O.Š.Antona Martina Slomška Vrhnika Predmet: Fizika Copyright by: Doman Blagojević www.cd-copy.tk Jupiter je peti planet od Sonca in daleč največji. Jupitrova masa je več
Microsoft Word - Astronomija-Projekt19fin
 Univerza v Ljubljani Fakulteta za matematiko in fiziko Jure Hribar, Rok Capuder Radialna odvisnost površinske svetlosti za eliptične galaksije Projektna naloga pri predmetu astronomija Ljubljana, april
Univerza v Ljubljani Fakulteta za matematiko in fiziko Jure Hribar, Rok Capuder Radialna odvisnost površinske svetlosti za eliptične galaksije Projektna naloga pri predmetu astronomija Ljubljana, april
PREDMETNI KURIKULUM ZA RAZVOJ METEMATIČNIH KOMPETENC
 MATEMATIKA 1.razred OSNOVE PREDMETA POKAZATELJI ZNANJA SPRETNOSTI KOMPETENCE Naravna števila -pozna štiri osnovne računske operacije in njihove lastnosti, -izračuna številske izraze z uporabo štirih računskih
MATEMATIKA 1.razred OSNOVE PREDMETA POKAZATELJI ZNANJA SPRETNOSTI KOMPETENCE Naravna števila -pozna štiri osnovne računske operacije in njihove lastnosti, -izračuna številske izraze z uporabo štirih računskih
Prevodnik_v_polju_14_
 14. Prevodnik v električnem polju Vsebina poglavja: prevodnik v zunanjem električnem polju, površina prevodnika je ekvipotencialna ploskev, elektrostatična indukcija (influenca), polje znotraj votline
14. Prevodnik v električnem polju Vsebina poglavja: prevodnik v zunanjem električnem polju, površina prevodnika je ekvipotencialna ploskev, elektrostatična indukcija (influenca), polje znotraj votline
M
 Š i f r a k a n d i d a t a : Državni izpitni center *M18153112* SPOMLADANSKI IZPITNI ROK FILOZOFIJA Izpitna pola 2 Esej Sreda, 30. maj 2018 / 120 minut Dovoljeno gradivo in pripomočki: Kandidat prinese
Š i f r a k a n d i d a t a : Državni izpitni center *M18153112* SPOMLADANSKI IZPITNI ROK FILOZOFIJA Izpitna pola 2 Esej Sreda, 30. maj 2018 / 120 minut Dovoljeno gradivo in pripomočki: Kandidat prinese
N
 Državni izpitni center *N19141132* 9. razred FIZIKA Ponedeljek, 13. maj 2019 NAVODILA ZA VREDNOTENJE NACIONALNO PREVERJANJE ZNANJA v 9. razredu Državni izpitni center Vse pravice pridržane. 2 N191-411-3-2
Državni izpitni center *N19141132* 9. razred FIZIKA Ponedeljek, 13. maj 2019 NAVODILA ZA VREDNOTENJE NACIONALNO PREVERJANJE ZNANJA v 9. razredu Državni izpitni center Vse pravice pridržane. 2 N191-411-3-2
TOTP - Fizika 2017/18 Seznam obravnavanih vsebin January 19, 2018 Ta seznam vsebin ne nadomešča zapiskov s predavanj. Je pa izčrpen spisek tega, kar s
 TOTP - Fizika 2017/18 Seznam obravnavanih vsebin January 19, 2018 Ta seznam vsebin ne nadomešča zapiskov s predavanj. Je pa izčrpen spisek tega, kar smo obravnavali. Vektorske količine so označene krepko.
TOTP - Fizika 2017/18 Seznam obravnavanih vsebin January 19, 2018 Ta seznam vsebin ne nadomešča zapiskov s predavanj. Je pa izčrpen spisek tega, kar smo obravnavali. Vektorske količine so označene krepko.
DN5(Kor).dvi
 Koreni Število x, ki reši enačbo x n = a, imenujemo n-ti koren števila a in to označimo z n a. Pri tem je n naravno število, a pa poljubno realno število. x = n a x n = a. ( n a ) n = a. ( n a ) m = n
Koreni Število x, ki reši enačbo x n = a, imenujemo n-ti koren števila a in to označimo z n a. Pri tem je n naravno število, a pa poljubno realno število. x = n a x n = a. ( n a ) n = a. ( n a ) m = n
30 Vpihovalne šobe Vpihovalna šoba VŠ-4 Uporaba Vpihovalne šobe VŠ-4 se uporabljajo za oskrbovanje prostorov s hladnim ali toplim zrakom povsod tam, k
 30 Vpihovalna šoba VŠ-4 Uporaba VŠ-4 se uporabljajo za oskrbovanje prostorov s hladnim ali toplim zrakom povsod tam, kjer se zahtevajo velike dometne razdalje in nizka stopnja šumnosti. S postavitvijo
30 Vpihovalna šoba VŠ-4 Uporaba VŠ-4 se uporabljajo za oskrbovanje prostorov s hladnim ali toplim zrakom povsod tam, kjer se zahtevajo velike dometne razdalje in nizka stopnja šumnosti. S postavitvijo
P182C10111
 Š i f r a k a n d i d a t a : Državni izpitni center *P18C10111* JESENSKI IZPITNI ROK MATEMATIKA Izpitna pola Ponedeljek, 7. avgust 018 / 10 minut Dovoljeno gradivo in pripomočki: Kandidat prinese nalivno
Š i f r a k a n d i d a t a : Državni izpitni center *P18C10111* JESENSKI IZPITNI ROK MATEMATIKA Izpitna pola Ponedeljek, 7. avgust 018 / 10 minut Dovoljeno gradivo in pripomočki: Kandidat prinese nalivno
SESTAVA VSEBINE MATEMATIKE V 6
 SESTAVA VSEBINE MATEMATIKE V 6. RAZREDU DEVETLETKE 1. KONFERENCA Št. ure Učne enote CILJI UVOD (1 ura) 1 Uvodna ura spoznati vsebine učnega načrta, način dela, učne pripomočke za pouk matematike v 6. razredu
SESTAVA VSEBINE MATEMATIKE V 6. RAZREDU DEVETLETKE 1. KONFERENCA Št. ure Učne enote CILJI UVOD (1 ura) 1 Uvodna ura spoznati vsebine učnega načrta, način dela, učne pripomočke za pouk matematike v 6. razredu
15. Seminar Optične Komunikacije Laboratorij za Sevanje in Optiko Fakulteta za Elektrotehniko Ljubljana, 30.jan - 1.feb 2008 Osnovne omejitve svetlobn
 15. Seminar Optične Komunikacije Laboratorij za Sevanje in Optiko Fakulteta za Elektrotehniko Ljubljana, 30.jan - 1.feb 2008 Osnovne omejitve svetlobnega vlakna Matjaž Vidmar Seznam prosojnic: Slika 1
15. Seminar Optične Komunikacije Laboratorij za Sevanje in Optiko Fakulteta za Elektrotehniko Ljubljana, 30.jan - 1.feb 2008 Osnovne omejitve svetlobnega vlakna Matjaž Vidmar Seznam prosojnic: Slika 1
TLAK PLOŠČINA 1. Zapiši oznako in enoto za ploščino. 2. Zapiši pretvornik pri ploščini in po velikosti zapiši enote od mm 2 do km Nariši skico z
 TLAK PLOŠČINA 1. Zapiši oznako in enoto za ploščino. 2. Zapiši pretvornik pri ploščini in po velikosti zapiši enote od mm 2 do km 2. 3. Nariši skico za kvadrat in zapiši, kako bi izračunal ploščino kvadrata.
TLAK PLOŠČINA 1. Zapiši oznako in enoto za ploščino. 2. Zapiši pretvornik pri ploščini in po velikosti zapiši enote od mm 2 do km 2. 3. Nariši skico za kvadrat in zapiši, kako bi izračunal ploščino kvadrata.
Funkcije in grafi
 14 Funkcije in grafi Funkcije Zapisi funkcij Sorazmernost Obratna sorazmernost Potenčne funkcije Polinomske funkcije Druge funkcije Prileganje podatkom 14.1 Funkcije Spremenljivke Odvisnost spremenljivk
14 Funkcije in grafi Funkcije Zapisi funkcij Sorazmernost Obratna sorazmernost Potenčne funkcije Polinomske funkcije Druge funkcije Prileganje podatkom 14.1 Funkcije Spremenljivke Odvisnost spremenljivk
izr12
 NARAVOSLOVNI POSTOPKI Kako uporabiti izkušnje, kako ravnati s podatki, kako sklepati in razlagati? Za to zbirko procesnih znanj se je uveljavilo poimenovanje naravoslovni postopki. To so: opazovanje, razvrščanje,
NARAVOSLOVNI POSTOPKI Kako uporabiti izkušnje, kako ravnati s podatki, kako sklepati in razlagati? Za to zbirko procesnih znanj se je uveljavilo poimenovanje naravoslovni postopki. To so: opazovanje, razvrščanje,
Matematika 2
 Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 23. april 2014 Soda in liha Fourierjeva vrsta Opomba Pri razvoju sode periodične funkcije f v Fourierjevo vrsto v razvoju nastopajo
Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 23. april 2014 Soda in liha Fourierjeva vrsta Opomba Pri razvoju sode periodične funkcije f v Fourierjevo vrsto v razvoju nastopajo
rm.dvi
 1 2 3 4 5 6 7 Ime, priimek Razred 14. DRŽAVNO TEKMOVANJE V RAZVEDRILNI MATEMATIKI NALOGE ZA PETI IN ŠESTI RAZRED OSNOVNE ŠOLE Čas reševanja nalog: 90 minut Točkovanje 1., 2., in 7. naloge je opisano v
1 2 3 4 5 6 7 Ime, priimek Razred 14. DRŽAVNO TEKMOVANJE V RAZVEDRILNI MATEMATIKI NALOGE ZA PETI IN ŠESTI RAZRED OSNOVNE ŠOLE Čas reševanja nalog: 90 minut Točkovanje 1., 2., in 7. naloge je opisano v
NAVADNA (BIVARIATNA) LINEARNA REGRESIJA O regresijski analizi govorimo, kadar želimo opisati povezanost dveh numeričnih spremenljivk. Opravka imamo to
 NAVADNA (BIVARIATNA) LINEARNA REGRESIJA O regresijski analizi govorimo, kadar želimo opisati povezanost dveh numeričnih spremenljivk. Opravka imamo torej s pari podatkov (x i,y i ), kjer so x i vrednosti
NAVADNA (BIVARIATNA) LINEARNA REGRESIJA O regresijski analizi govorimo, kadar želimo opisati povezanost dveh numeričnih spremenljivk. Opravka imamo torej s pari podatkov (x i,y i ), kjer so x i vrednosti
Univerza na Primorskem FAMNIT, MFI Vrednotenje zavarovalnih produktov Seminarska naloga Naloge so sestavni del preverjanja znanja pri predmetu Vrednot
 Univerza na Primorskem FAMNIT, MFI Vrednotenje zavarovalnih produktov Seminarska naloga Naloge so sestavni del preverjanja znanja pri predmetu Vrednotenje zavarovalnih produktov. Vsaka naloga je vredna
Univerza na Primorskem FAMNIT, MFI Vrednotenje zavarovalnih produktov Seminarska naloga Naloge so sestavni del preverjanja znanja pri predmetu Vrednotenje zavarovalnih produktov. Vsaka naloga je vredna
Slide 1
 Vsak vektor na premici skozi izhodišče lahko zapišemo kot kjer je v smerni vektor premice in a poljubno število. r a v Vsak vektor na ravnini skozi izhodišče lahko zapišemo kot kjer sta v, v vektorja na
Vsak vektor na premici skozi izhodišče lahko zapišemo kot kjer je v smerni vektor premice in a poljubno število. r a v Vsak vektor na ravnini skozi izhodišče lahko zapišemo kot kjer sta v, v vektorja na
Poročilo za 1. del seminarske naloge- igrica Kača Opis igrice Kača (Snake) je klasična igrica, pogosto prednaložena na malce starejših mobilnih telefo
 Poročilo za 1. del seminarske naloge- igrica Kača Opis igrice Kača (Snake) je klasična igrica, pogosto prednaložena na malce starejših mobilnih telefonih. Obstaja precej različic, sam pa sem sestavil meni
Poročilo za 1. del seminarske naloge- igrica Kača Opis igrice Kača (Snake) je klasična igrica, pogosto prednaložena na malce starejših mobilnih telefonih. Obstaja precej različic, sam pa sem sestavil meni
Brownova kovariancna razdalja
 Brownova kovariančna razdalja Nace Čebulj Fakulteta za matematiko in fiziko 8. januar 2015 Nova mera odvisnosti Motivacija in definicija S primerno izbiro funkcije uteži w(t, s) lahko definiramo mero odvisnosti
Brownova kovariančna razdalja Nace Čebulj Fakulteta za matematiko in fiziko 8. januar 2015 Nova mera odvisnosti Motivacija in definicija S primerno izbiro funkcije uteži w(t, s) lahko definiramo mero odvisnosti
Microsoft Word - Analiza rezultatov NPZ matematika 2018.docx
 Analiza dosežkov pri predmetu matematika za NPZ 28 6. razred NPZ matematika 28 Dosežek šole Povprečno število točk v % Državno povprečje Povprečno število točk v % Odstopanje v % 49,55 52,52 2,97 Povprečni
Analiza dosežkov pri predmetu matematika za NPZ 28 6. razred NPZ matematika 28 Dosežek šole Povprečno število točk v % Državno povprečje Povprečno število točk v % Odstopanje v % 49,55 52,52 2,97 Povprečni
POPOLNI KVADER
 List za mlade matematike, fizike, astronome in računalnikarje ISSN 031-662 Letnik 18 (1990/1991) Številka 3 Strani 134 139 Edvard Kramar: POPOLNI KVADER Ključne besede: matematika, geometrija, kvader,
List za mlade matematike, fizike, astronome in računalnikarje ISSN 031-662 Letnik 18 (1990/1991) Številka 3 Strani 134 139 Edvard Kramar: POPOLNI KVADER Ključne besede: matematika, geometrija, kvader,
Vaje: Matrike 1. Ugani rezultat, nato pa dokaži z indukcijo: (a) (b) [ ] n 1 1 ; n N 0 1 n ; n N Pokaži, da je množica x 0 y 0 x
![Vaje: Matrike 1. Ugani rezultat, nato pa dokaži z indukcijo: (a) (b) [ ] n 1 1 ; n N 0 1 n ; n N Pokaži, da je množica x 0 y 0 x Vaje: Matrike 1. Ugani rezultat, nato pa dokaži z indukcijo: (a) (b) [ ] n 1 1 ; n N 0 1 n ; n N Pokaži, da je množica x 0 y 0 x](/thumbs/99/142441276.jpg) Vaje: Matrike 1 Ugani rezultat, nato pa dokaži z indukcijo: (a) (b) [ ] n 1 1 ; n N n 1 1 0 1 ; n N 0 2 Pokaži, da je množica x 0 y 0 x y x + z ; x, y, z R y x z x vektorski podprostor v prostoru matrik
Vaje: Matrike 1 Ugani rezultat, nato pa dokaži z indukcijo: (a) (b) [ ] n 1 1 ; n N n 1 1 0 1 ; n N 0 2 Pokaži, da je množica x 0 y 0 x y x + z ; x, y, z R y x z x vektorski podprostor v prostoru matrik
Naloge 1. Dva električna grelnika z ohmskima upornostma 60 Ω in 30 Ω vežemo vzporedno in priključimo na idealni enosmerni tokovni vir s tokom 10 A. Tr
 Naloge 1. Dva električna grelnika z ohmskima upornostma 60 Ω in 30 Ω vežemo vzporedno in priključimo na idealni enosmerni tokovni vir s tokom 10 A. Trditev: idealni enosmerni tokovni vir obratuje z močjo
Naloge 1. Dva električna grelnika z ohmskima upornostma 60 Ω in 30 Ω vežemo vzporedno in priključimo na idealni enosmerni tokovni vir s tokom 10 A. Trditev: idealni enosmerni tokovni vir obratuje z močjo
M
 Š i f r a k a n d i d a t a : Državni izpitni center *M16140111* Osnovna raven MATEMATIKA Izpitna pola 1 SPOMLADANSKI IZPITNI ROK Sobota, 4. junij 016 / 10 minut Dovoljeno gradivo in pripomočki: Kandidat
Š i f r a k a n d i d a t a : Državni izpitni center *M16140111* Osnovna raven MATEMATIKA Izpitna pola 1 SPOMLADANSKI IZPITNI ROK Sobota, 4. junij 016 / 10 minut Dovoljeno gradivo in pripomočki: Kandidat
Ime in priimek: Vpisna št: FAKULTETA ZA MATEMATIKO IN FIZIKO Oddelek za matematiko Statistika Pisni izpit 31. avgust 2018 Navodila Pazljivo preberite
 Ime in priimek: Vpisna št: FAKULTETA ZA MATEMATIKO IN FIZIKO Oddelek za matematiko Statistika Pisni izpit 31 avgust 018 Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja Za pozitiven
Ime in priimek: Vpisna št: FAKULTETA ZA MATEMATIKO IN FIZIKO Oddelek za matematiko Statistika Pisni izpit 31 avgust 018 Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja Za pozitiven
P181C10111
 Š i f r a k a n d i d a t a : Državni izpitni center *P181C10111* SPOMLADANSKI IZPITNI ROK MATEMATIKA Izpitna pola Sobota, 9. junij 018 / 10 minut Dovoljeno gradivo in pripomočki: Kandidat prinese nalivno
Š i f r a k a n d i d a t a : Državni izpitni center *P181C10111* SPOMLADANSKI IZPITNI ROK MATEMATIKA Izpitna pola Sobota, 9. junij 018 / 10 minut Dovoljeno gradivo in pripomočki: Kandidat prinese nalivno
Opisi območij rezultatov NPZ
 Predmetna komisija za fiziko Opisi dosežkov učencev 9. razreda na nacionalnem preverjanju znanja Slika: Porazdelitev točk pri fiziki, 9. razred Uvodni komentar Pri sestavljanju nalog je PK za fiziko upoštevala,
Predmetna komisija za fiziko Opisi dosežkov učencev 9. razreda na nacionalnem preverjanju znanja Slika: Porazdelitev točk pri fiziki, 9. razred Uvodni komentar Pri sestavljanju nalog je PK za fiziko upoštevala,
Opisi območij rezultatov NPZ
 Predmetna komisija za fiziko Opisi dosežkov učencev 9. razreda pri NPZ-ju Slika: Porazdelitev točk pri fiziki, 9. razred Uvodni komentar Pri sestavljanju nalog je PK za fiziko upoštevala, da pomeni znanje
Predmetna komisija za fiziko Opisi dosežkov učencev 9. razreda pri NPZ-ju Slika: Porazdelitev točk pri fiziki, 9. razred Uvodni komentar Pri sestavljanju nalog je PK za fiziko upoštevala, da pomeni znanje
Strokovni izobraževalni center Ljubljana, Srednja poklicna in strokovna šola Bežigrad PRIPRAVE NA PISNI DEL IZPITA IZ MATEMATIKE 2. letnik nižjega pok
 Strokovni izobraževalni center Ljubljana, Srednja poklicna in strokovna šola Bežigrad PRIPRAVE NA PISNI DEL IZPITA IZ MATEMATIKE 2. letnik nižjega poklicnega izobraževanja NAVODILA: Izpit iz matematike
Strokovni izobraževalni center Ljubljana, Srednja poklicna in strokovna šola Bežigrad PRIPRAVE NA PISNI DEL IZPITA IZ MATEMATIKE 2. letnik nižjega poklicnega izobraževanja NAVODILA: Izpit iz matematike
PowerPoint Presentation
 Integral rešujemo nalogo: Dana je funkcija f. Najdimo funkcijo F, katere odvod je enak f. Če je F ()=f() pravimo, da je F() primitivna funkcija za funkcijo f(). Primeri: f ( ) = cos f ( ) = sin f () =
Integral rešujemo nalogo: Dana je funkcija f. Najdimo funkcijo F, katere odvod je enak f. Če je F ()=f() pravimo, da je F() primitivna funkcija za funkcijo f(). Primeri: f ( ) = cos f ( ) = sin f () =
1
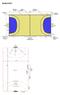 ROKOMET IGRIŠČE Igrišče je pravokotnik, dolg 40m in širok 20m. Sestavljen je iz dveh enakih polj za igro in dveh vratarjevih prostorov. Daljši stranici se imenujeta vzdolžne črte, krajše pa prečne črte
ROKOMET IGRIŠČE Igrišče je pravokotnik, dolg 40m in širok 20m. Sestavljen je iz dveh enakih polj za igro in dveh vratarjevih prostorov. Daljši stranici se imenujeta vzdolžne črte, krajše pa prečne črte
LaTeX slides
 Linearni in nelinearni modeli Milena Kovač 22. december 2006 Biometrija 2006/2007 1 Linearni, pogojno linearni in nelinearni modeli Kriteriji za razdelitev: prvi parcialni odvodi po parametrih Linearni
Linearni in nelinearni modeli Milena Kovač 22. december 2006 Biometrija 2006/2007 1 Linearni, pogojno linearni in nelinearni modeli Kriteriji za razdelitev: prvi parcialni odvodi po parametrih Linearni
VETRNO KOLO
 VETRNO KOLO KAZALO: Zgodovina Razvoj vetrnic Vrste vetrnic Značilnosti Uporaba Sestavni deli Delovanje Animacije Prednosti in slabosti Viri in literatura ZGODOVINA: Ljudje izkoriščamo energijo vetra že
VETRNO KOLO KAZALO: Zgodovina Razvoj vetrnic Vrste vetrnic Značilnosti Uporaba Sestavni deli Delovanje Animacije Prednosti in slabosti Viri in literatura ZGODOVINA: Ljudje izkoriščamo energijo vetra že
VPRAŠALNIK BRALNE MOTIVACIJE ZA MLAJŠE UČENCE –
 PRAŠALNIK BRALNE MOTIACIJE ZA STAREJŠE UČENCE BM-st Pred teboj je vprašalnik o branju. Prosimo te, da nanj odgovoriš tako, kot velja zate. vprašalniku ni pravilnih oz. napačnih odgovorov. Na posamezne
PRAŠALNIK BRALNE MOTIACIJE ZA STAREJŠE UČENCE BM-st Pred teboj je vprašalnik o branju. Prosimo te, da nanj odgovoriš tako, kot velja zate. vprašalniku ni pravilnih oz. napačnih odgovorov. Na posamezne
Univerza v Ljubljani Naravoslovnotehniška fakulteta Oddelek za tekstilstvo Sledenje pogledu (Eye tracking) Seminarska naloga pri predmetu Interaktivni
 Univerza v Ljubljani Naravoslovnotehniška fakulteta Oddelek za tekstilstvo Sledenje pogledu (Eye tracking) Seminarska naloga pri predmetu Interaktivni mediji Smer študija: Načrtovanje tekstilij in oblačil,
Univerza v Ljubljani Naravoslovnotehniška fakulteta Oddelek za tekstilstvo Sledenje pogledu (Eye tracking) Seminarska naloga pri predmetu Interaktivni mediji Smer študija: Načrtovanje tekstilij in oblačil,
Univerza v Ljubljani FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO Tržaška c. 25, 1000 Ljubljana Realizacija n-bitnega polnega seštevalnika z uporabo kvan
 Univerza v Ljubljani FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO Tržaška c. 25, 1000 Ljubljana Realizacija n-bitnega polnega seštevalnika z uporabo kvantnih celičnih avtomatov SEMINARSKA NALOGA Univerzitetna
Univerza v Ljubljani FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO Tržaška c. 25, 1000 Ljubljana Realizacija n-bitnega polnega seštevalnika z uporabo kvantnih celičnih avtomatov SEMINARSKA NALOGA Univerzitetna
Diapozitiv 1
 Vhodno-izhodne naprave naprave 1 Uvod VIN - 1 2018, Igor Škraba, FRI Vsebina 1 Uvod Signal električni signal Zvezni signal Diskretni signal Digitalni signal Lastnosti prenosnih medijev Slabljenje Pasovna
Vhodno-izhodne naprave naprave 1 Uvod VIN - 1 2018, Igor Škraba, FRI Vsebina 1 Uvod Signal električni signal Zvezni signal Diskretni signal Digitalni signal Lastnosti prenosnih medijev Slabljenje Pasovna
Matematika II (UN) 2. kolokvij (7. junij 2013) RE ITVE Naloga 1 (25 to k) ƒasovna funkcija f je denirana za t [0, 2] in podana s spodnjim grafom. f t
![Matematika II (UN) 2. kolokvij (7. junij 2013) RE ITVE Naloga 1 (25 to k) ƒasovna funkcija f je denirana za t [0, 2] in podana s spodnjim grafom. f t Matematika II (UN) 2. kolokvij (7. junij 2013) RE ITVE Naloga 1 (25 to k) ƒasovna funkcija f je denirana za t [0, 2] in podana s spodnjim grafom. f t](/thumbs/102/155599169.jpg) Matematika II (UN) 2. kolokvij (7. junij 2013) RE ITVE Naloga 1 (25 to k) ƒasovna funkcija f je denirana za t [0, 2] in podana s spodnjim grafom. f t 0.5 1.5 2.0 t a.) Nari²ite tri grafe: graf (klasi ne)
Matematika II (UN) 2. kolokvij (7. junij 2013) RE ITVE Naloga 1 (25 to k) ƒasovna funkcija f je denirana za t [0, 2] in podana s spodnjim grafom. f t 0.5 1.5 2.0 t a.) Nari²ite tri grafe: graf (klasi ne)
glava.dvi
 Lastnosti verjetnosti 1. Za dogodka A in B velja: P(A B) = P(A) + P(B) P(A B) 2. Za dogodke A, B in C velja: P(A B C) = P(A) + P(B) + P(C) P(A B) P(A C) P(B C) + P(A B C) Kako lahko to pravilo posplošimo
Lastnosti verjetnosti 1. Za dogodka A in B velja: P(A B) = P(A) + P(B) P(A B) 2. Za dogodke A, B in C velja: P(A B C) = P(A) + P(B) + P(C) P(A B) P(A C) P(B C) + P(A B C) Kako lahko to pravilo posplošimo
PowerPointova predstavitev
 U K 20 P K U P M 2 0 1 2 12 M OBLIKOVANJE POJMA ŠTEVILO PRI OTROKU V 1. RAZREDU Sonja Flere, Mladen Kopasid Konferenca o učenju in poučevanju matematike, M a r i b o r, 2 3. i n 2 4. avgusta 2 0 1 2 Oblikovanje
U K 20 P K U P M 2 0 1 2 12 M OBLIKOVANJE POJMA ŠTEVILO PRI OTROKU V 1. RAZREDU Sonja Flere, Mladen Kopasid Konferenca o učenju in poučevanju matematike, M a r i b o r, 2 3. i n 2 4. avgusta 2 0 1 2 Oblikovanje
P r e d m e t n i k Seznam skupnih izbirnih predmetov v študijskem programu Izbirni predmeti Zap. št. Predmet Nosilec Kontaktne ure Klinične Pred. Sem
 P r e d m e t n i k Seznam skupnih izbirnih predmetov v študijskem programu 001 Akustika in ultrazvok Jurij Prezelj 002 Diferencialne enačbe Aljoša Peperko 003 Eksperimentalne metode v nosilec bo znan
P r e d m e t n i k Seznam skupnih izbirnih predmetov v študijskem programu 001 Akustika in ultrazvok Jurij Prezelj 002 Diferencialne enačbe Aljoša Peperko 003 Eksperimentalne metode v nosilec bo znan
CpE & ME 519
 2D Transformacije Zakaj potrebujemo transformacije? Animacija Več instanc istega predmeta, variacije istega objekta na sceni Tvorba kompliciranih predmetov iz bolj preprostih Transformacije gledanja Kaj
2D Transformacije Zakaj potrebujemo transformacije? Animacija Več instanc istega predmeta, variacije istega objekta na sceni Tvorba kompliciranih predmetov iz bolj preprostih Transformacije gledanja Kaj
10. Meritev šumnega števila ojačevalnika Vsako radijsko zvezo načrtujemo za zahtevano razmerje signal/šum. Šum ima vsaj dva izvora: naravni šum T A, k
 10. Meritev šumnega števila ojačevalnika Vsako radijsko zvezo načrtujemo za zahtevano razmerje signal/šum. Šum ima vsaj dva izvora: naravni šum T A, ki ga sprejme antena in dodatni šum T S radijskega sprejemnika.
10. Meritev šumnega števila ojačevalnika Vsako radijsko zvezo načrtujemo za zahtevano razmerje signal/šum. Šum ima vsaj dva izvora: naravni šum T A, ki ga sprejme antena in dodatni šum T S radijskega sprejemnika.
N
 Državni izpitni center *N15164132* 9. razred TEHNIKA IN TEHNOLOGIJA Ponedeljek, 11. maj 2015 NAVODILA ZA VREDNOTENJE NACIONALNO PREVERJANJE ZNANJA 9. razred RIC 2015 2 N151-641-3-2 SPLOŠNA NAVODILA Prosimo,
Državni izpitni center *N15164132* 9. razred TEHNIKA IN TEHNOLOGIJA Ponedeljek, 11. maj 2015 NAVODILA ZA VREDNOTENJE NACIONALNO PREVERJANJE ZNANJA 9. razred RIC 2015 2 N151-641-3-2 SPLOŠNA NAVODILA Prosimo,
Microsoft Word - M
 Državni izpitni center *M773* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Četrtek, 4. junij SPLOŠNA MATRA RIC M-77--3 IZPITNA POLA ' ' Q Q ( Q Q)/ Zapisan izraz za naboja ' ' 6 6 6 Q Q (6 4 ) / C
Državni izpitni center *M773* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Četrtek, 4. junij SPLOŠNA MATRA RIC M-77--3 IZPITNA POLA ' ' Q Q ( Q Q)/ Zapisan izraz za naboja ' ' 6 6 6 Q Q (6 4 ) / C
Srednja šola za oblikovanje
 Srednja šola za oblikovanje Park mladih 8 2000 Maribor POKLICNA MATURA MATEMATIKA SEZNAM VPRAŠANJ ZA USTNI DEL NARAVNA IN CELA ŠTEVILA Opišite vrstni red računskih operacij v množici naravnih števil. Kakšen
Srednja šola za oblikovanje Park mladih 8 2000 Maribor POKLICNA MATURA MATEMATIKA SEZNAM VPRAŠANJ ZA USTNI DEL NARAVNA IN CELA ŠTEVILA Opišite vrstni red računskih operacij v množici naravnih števil. Kakšen
Microsoft Word - UP_Lekcija04_2014.docx
 4. Zanka while Zanke pri programiranju uporabljamo, kadar moramo stavek ali skupino stavkov izvršiti večkrat zaporedoma. Namesto, da iste (ali podobne) stavke pišemo n-krat, jih napišemo samo enkrat in
4. Zanka while Zanke pri programiranju uporabljamo, kadar moramo stavek ali skupino stavkov izvršiti večkrat zaporedoma. Namesto, da iste (ali podobne) stavke pišemo n-krat, jih napišemo samo enkrat in
(Microsoft Word - 3. Pogre\232ki in negotovost-c.doc)
 3.4 Merilna negotovost Merilna negotovost je parameter, ki pripada merilnem rezltat. Označje razpršenost vrednosti, ki jih je mogoče z določeno verjetnostjo pripisati merjeni veličini. Navaja kakovost
3.4 Merilna negotovost Merilna negotovost je parameter, ki pripada merilnem rezltat. Označje razpršenost vrednosti, ki jih je mogoče z določeno verjetnostjo pripisati merjeni veličini. Navaja kakovost
Ime in priimek: Vpisna št: FAKULTETA ZA MATEMATIKO IN FIZIKO Oddelek za matematiko Statistika Pisni izpit 6. julij 2018 Navodila Pazljivo preberite be
 Ime in priimek: Vpisna št: FAKULEA ZA MAEMAIKO IN FIZIKO Oddelek za matematiko Statistika Pisni izpit 6 julij 2018 Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja Za pozitiven rezultat
Ime in priimek: Vpisna št: FAKULEA ZA MAEMAIKO IN FIZIKO Oddelek za matematiko Statistika Pisni izpit 6 julij 2018 Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja Za pozitiven rezultat
Microsoft Word - N _moderacija.docx
 2 N151-401-2-2 SPLOŠNA NAVODILA Prosimo, da moderirano različico navodil za vrednotenje dosledno upoštevate. Če učenec pravilno reši nalogo na svoj način (ki je matematično korekten) in je to razvidno
2 N151-401-2-2 SPLOŠNA NAVODILA Prosimo, da moderirano različico navodil za vrednotenje dosledno upoštevate. Če učenec pravilno reši nalogo na svoj način (ki je matematično korekten) in je to razvidno
11. Navadne diferencialne enačbe Začetni problem prvega reda Iščemo funkcijo y(x), ki zadošča diferencialni enačbi y = f(x, y) in začetnemu pogo
 11. Navadne diferencialne enačbe 11.1. Začetni problem prvega reda Iščemo funkcijo y(x), ki zadošča diferencialni enačbi y = f(x, y) in začetnemu pogoju y(x 0 ) = y 0, kjer je f dana dovolj gladka funkcija
11. Navadne diferencialne enačbe 11.1. Začetni problem prvega reda Iščemo funkcijo y(x), ki zadošča diferencialni enačbi y = f(x, y) in začetnemu pogoju y(x 0 ) = y 0, kjer je f dana dovolj gladka funkcija
Moj poskus formativnega spremljanja
 Moj poskus formativnega spremljanja Nada Žonta Kropivšek, marec 2019 10 let OŠ Vič, 17 let Gimnazija Poljane, splošna gimnazija Okoli 10 let pripravljam za maturo iz fizike Od moje klasike do drugačnih
Moj poskus formativnega spremljanja Nada Žonta Kropivšek, marec 2019 10 let OŠ Vič, 17 let Gimnazija Poljane, splošna gimnazija Okoli 10 let pripravljam za maturo iz fizike Od moje klasike do drugačnih
STAVKI _5_
 5. Stavki (Teoremi) Vsebina: Stavek superpozicije, stavek Thévenina in Nortona, maksimalna moč na bremenu (drugič), stavek Tellegena. 1. Stavek superpozicije Ta stavek določa, da lahko poljubno vezje sestavljeno
5. Stavki (Teoremi) Vsebina: Stavek superpozicije, stavek Thévenina in Nortona, maksimalna moč na bremenu (drugič), stavek Tellegena. 1. Stavek superpozicije Ta stavek določa, da lahko poljubno vezje sestavljeno
VIDEOANALIZA GIBANJ Za kratke projektne naloge lahko dijaki z domačimi digitalnimi fotoaparati posnamejo nekaj sekundne videofilme poljubnih gibanj. U
 VIDEOANALIZA GIBANJ Za kratke projektne naloge lahko dijaki z domačimi digitalnimi fotoaparati posnamejo nekaj sekundne videofilme poljubnih gibanj. Uporabni so skoraj vsi domači digitalni fotoaparati.
VIDEOANALIZA GIBANJ Za kratke projektne naloge lahko dijaki z domačimi digitalnimi fotoaparati posnamejo nekaj sekundne videofilme poljubnih gibanj. Uporabni so skoraj vsi domači digitalni fotoaparati.
resitve.dvi
 FAKULTETA ZA STROJNIŠTVO Matematika 2. kolokvij 4. januar 212 Ime in priimek: Vpisna št: Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja. Veljale bodo samo rešitve na papirju, kjer
FAKULTETA ZA STROJNIŠTVO Matematika 2. kolokvij 4. januar 212 Ime in priimek: Vpisna št: Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja. Veljale bodo samo rešitve na papirju, kjer
PRIPRAVA NA 1. Š. N.: KVADRATNA FUNKCIJA IN KVADRATNA ENAČBA 1. Izračunaj presečišča parabole y=5 x x 8 s koordinatnima osema. R: 2 0, 8, 4,0,,0
 PRIPRAVA NA 1. Š. N.: KVADRATNA FUNKCIJA IN KVADRATNA ENAČBA 1. Izračunaj presečišča parabole y=5 x +18 x 8 s koordinatnima osema. R: 0, 8, 4,0,,0 5. Zapiši enačbo kvadratne funkcije f (x )=3 x +1 x+8
PRIPRAVA NA 1. Š. N.: KVADRATNA FUNKCIJA IN KVADRATNA ENAČBA 1. Izračunaj presečišča parabole y=5 x +18 x 8 s koordinatnima osema. R: 0, 8, 4,0,,0 5. Zapiši enačbo kvadratne funkcije f (x )=3 x +1 x+8
Popravki nalog: Numerična analiza - podiplomski študij FGG : popravljena naloga : popravljena naloga 14 domače naloge - 2. skupina
 Popravki nalog: Numerična analiza - podiplomski študij FGG 9.8.24: popravljena naloga 4 3..25: popravljena naloga 4 domače naloge - 2. skupina V drugem delu morate rešiti toliko nalog, da bo njihova skupna
Popravki nalog: Numerična analiza - podiplomski študij FGG 9.8.24: popravljena naloga 4 3..25: popravljena naloga 4 domače naloge - 2. skupina V drugem delu morate rešiti toliko nalog, da bo njihova skupna
Robert Hooke
 Robert Hooke Robert Hooke se je 18. julija leta 1635 rodil na otoku Wight v Freshwaterju v Angliji. Njegov oče je bil duhovnik, John Hooke, ki je deloval v cerkvi Vseh svetih. Pri Robertovih 10 letih je
Robert Hooke Robert Hooke se je 18. julija leta 1635 rodil na otoku Wight v Freshwaterju v Angliji. Njegov oče je bil duhovnik, John Hooke, ki je deloval v cerkvi Vseh svetih. Pri Robertovih 10 letih je
